| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- activation function
- Anaconda
- transfer learning
- Backbone network
- ImageNet
- pycharm
- pre trained model
- ReLU
- vggnet
- Today
- Total
Image 초보의 개발 공부
Activation Function 본문
Activation Function을 쓰는 이유
Neural Network가 진행되면 각 노드에 이전 노드에서 계산된 값들 또는 bias가 입력된다.
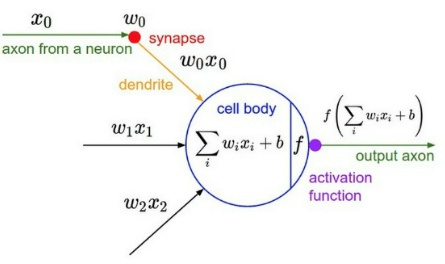
계산된 값은 노드에서 합해지며 다음 노드로 넘어간다. 이때 다음 노드로 전해지며 활성화 함수가 사용된다.
그렇다면 굳이 활성화 함수를 사용해서 다음 노드로 넘기는 이유가 무엇일까? 그 이유를 쉽게 말하면 모델을 복잡하게 만들기 위함이다. 다시 말해 hidden layer를 더 쌓기 위함이다. 이는 비선형(non linear)문제를 해결하는데 중요한 역할을 한다.
비선형 문제를 해결하기 위해 단층 퍼셉트론을 쌓는 방법을 이용했는데 hidden layer를 무작정 쌓는다고 비선형문제를 해결할 수는 없다. 하지만 활성화 함수를 이용하면 선형 분류기를 비선형 분류기로 만들 수 있다.
Neural network에서는 activation function으로 nonlinear fuction만을 이용하는데 linear function을 이용하면 layer를 많이 쌓는 의미가 없기 때문이다. 예를 들어, 활성화 함수$h(x) = cx$가 있다고 하자. 3층으로 구성된 network 라고 할 때, output = $ y(x) = h(h(h(x))) = c \times c \times c \times x = c^3 x $가 된다. 즉 활성화 함수$ h(x) = c^3 x $인 활성화 함수 one layer와 다를 바가 없어진다.
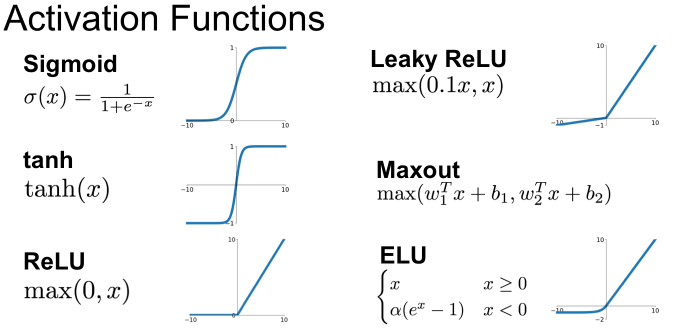
다음에는 다양한 활성화 함수에 대해 소개할 것이다.
Perceptron의 Activation function “Step function”

perceptron은 임계값을 경계로 출력이 바뀌는데 이는 step function을 활성화 함수로 사용하는 경우이다. 하지만 Step function은 XOR문제를 해결하지 못하는 문제를 가져 사용되지 않는다
Sigmoid
Neural Network에서 가중치를 학습 시킬 때 미분을 사용했기에 step function을 이용할 수 없었다. 또 step function은 0과 1의 이진화 값만 출력하기에 정보 손실 또한 있었다. 때문에 곡선 형태이며 연속적인 값을 갖는 sigmoid 함수가 사용되었다. 시그모이드 함수는 우리가 알고 있는 로지스틱 함수 $f(x)= {1 \over 1 + e^{-x}}$이다.
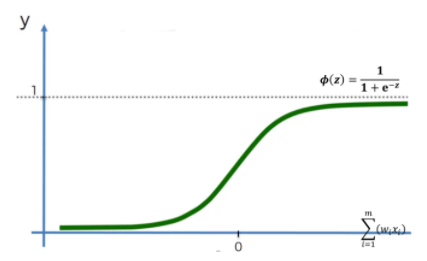
하지만 sigmoid 함수도 단점이 있어 현재는 잘 사용되지 않는다. sigmoi는 다음의 문제를 가진다.
- Gradient Vanishing Problem
층이 deep해질수록 backpropagation 수행 시 기울기가 소실되는(0이 되는) 문제가 발생한다.
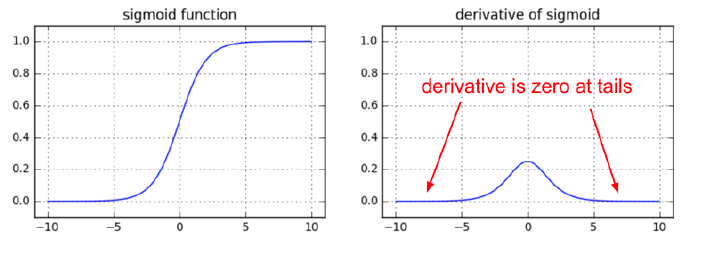
위 그림과 같이 함수의 미분 값이 최대값 0.25에서 더 커지지 않고 0에 수렴하기에 학습이 더이상 진행되지 않는다.
2. 함수값 중심이 0이 아니다.
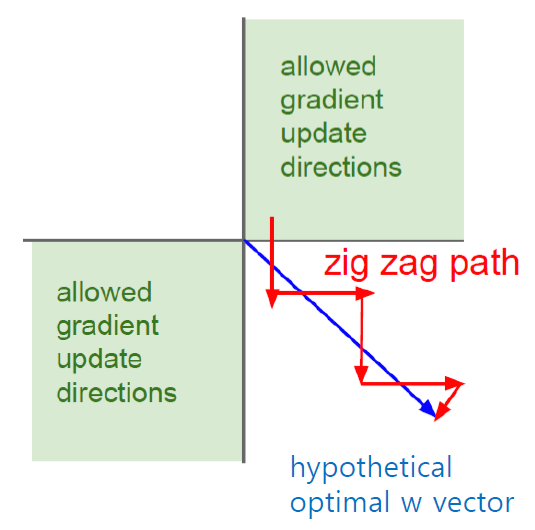
입력값이 항상 양수이기 때문에 가중치에 대한 기울기가 항상 양수 또는 음수가 되어 학습이 잘 안될 수 있다. (zigzag 문제)
sigmoid는 은닉층 활성화 함수로도 사용되지만 output function으로도 사용된다. 출력값이 둘로 정해져 있기에 이진 분류 문제에서 사용되기 때문이다.
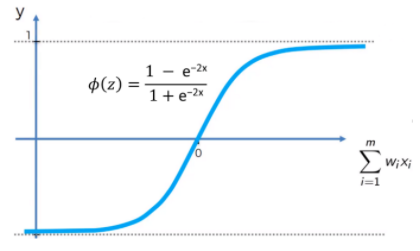
Hyperbolic Tangent(Tanh)
시그모이드 함수의 중심을 0으로 맞추기 위해 개선된 함수이다. 결과값이 (-1, 1) 사이이면서 출력의 양수 음수 비율이 비슷하기에 zigzag 문제가 덜 하다.
하지만 logistic function(sigmoid)과 형태가 비슷하기에 gradient vanishing problem을 해결하지 못한다. 또한 exp연산이 많아 시간이 오래걸린다.
Lu(Linear Unit function) Family
활성화 함수 중 ReLu function은 많은 문제를 해결하면서 여러 장단점이 있기에 여러 분화된 함수들을 가진다. 특히 Linear Unit의 형태를 가진 여러 함수가 등장했다.
ReLU
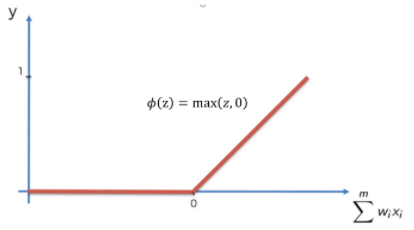
입력값이 양수일 경우 입력값 그대로를 전하는 함수이다. 때문에 vanishing gradient problem을 해결할 뿐만 아니라 미분계산이 훨씬 간단해졌기 때문에 sigmoid 나 tanh에 비해 손실함수의 수렴속도가 6배나 빠르다. 하지만 함수의 중앙이 0이 아니기 때문에 zigzag문제가 발생한다.
ReLU는 음수값들은 모조리 0으로 만들어버리기에 0 이하의 output을 가지는 노드들이 죽어버리는 현상이 발생한다. 이를 Dying ReLU 라고 부른다. 때문에 이를 해결하기 위해 다양한 ReLU를 변형한 함수들이 등장했다.
Dying ReLU현상이 있다 하지만 의외로 구조에 따라선 학습에 큰 영향을 끼치지 않는다고 한다. 자세한 내용은 아래에 잘 설명된 블로그를 첨부한다.
Leaky ReLU
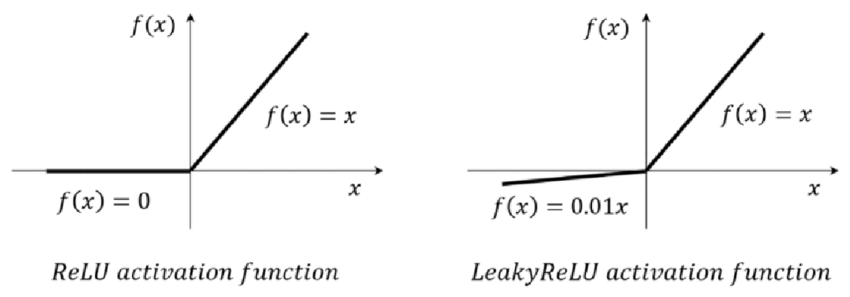
ReLU에서 함수의 중앙을 0으로 맞춰 Dying ReLU를 막고 zigzag 문제를 해결하기 위해 음수값에 0.01을 곱해 아주 작은 값으로 만든 것이 LeakyReLU이다.
그러나 음수 값에 대해 선형성이 생기게 되고 그로 인해 복잡한 분류문제를 해결할 수 없는 한계가 생겼다.
때문에 음수값이 매우 중요한 상황이 아니라면 제한적으로 사용하기 바란다.
PReLU(Parameter ReLU)
Leaky ReLU가 음수에 0.01을 곱해주었다면 PReLU는 곱하는 값을 하이퍼 파라미터로 주어 내가 원하는 값을 곱하는 것이다.
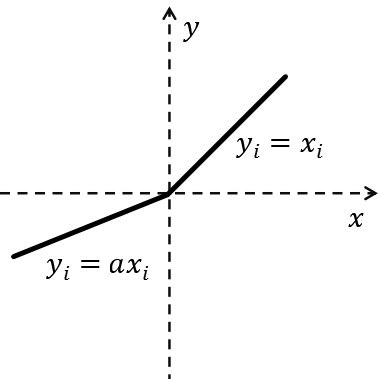
Leaky ReLU와 성격이 비슷하지만 계수를 가중치 매개변수처럼 학습되도록 역전파에 의해 값이 변형되기에 대규모 데이터셋에서는 ReLU보다 성능이 우세하다고 알려져 있지만 소규모 데이터셋에서는 여전히 weight explosion과 overfitting 위험이 있다.
또한 여전히 음수영역이 선형성을 띄므로 복잡한 분류문제를 처리하지 못할 수 있다.
ELU(Exponential Linear Unit)
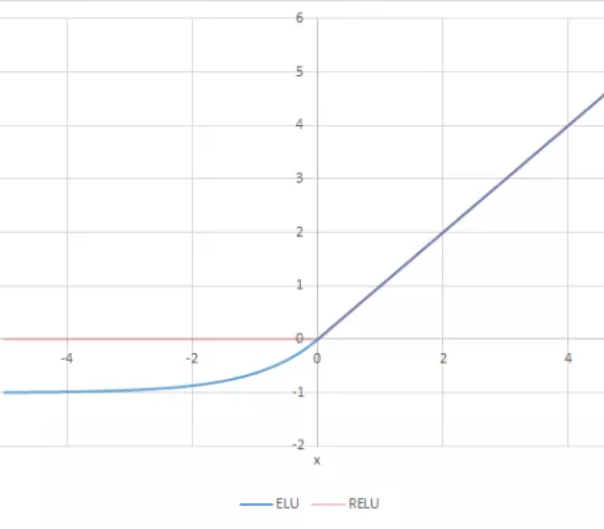
$$f(x) = x(x>0), \alpha(e^x-1) (x<0)$$
ReLU와 유사하지만 exp 연산을 통해 그래프를 부드럽게 이었다. 그로 인해 미분 시에도 ReLU와 달리 부드럽게 이어지게 된다.
ReLU의 대표적인 대안 중 하나로 음에서도 비선형적이기 때문에 복잡한 분류 문제를 해결할 수 있다. 일반적으로 $\alpha$를 1로 설정하고 이 경우 x=0에서 급격하게 변하지 않고 모든 구간에서 부드럽게 변하므로 경사하강법에서 수렴이 매우 빠르다고 한다.
그러나 ReLU에 비해 성능이 크게 늘어나지는 않고 되려 exp연산으로 인해 연산량이 많아져 잘 사용되지 않는다.
SELU(Scaled Exponential Linear Unit)
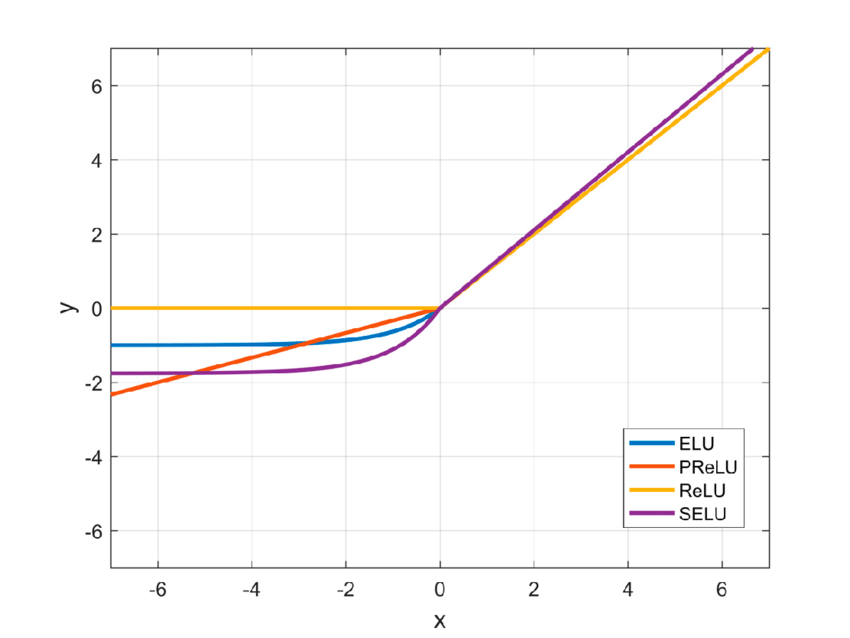
ELU에서 $\alpha$에 1을 넣으므로 PReLU와 비슷하게 $\alpha$를 하이퍼 파라미터로 바꾸어 학습으로 조정 가능하게 하였다.
$\alpha$ 2개를 파라미터로 넣어 학습시키면 활성화 함수의 분산이 일정하게 나와서 성능이 좋아진다고 한다. 그러나 $\alpha$값에 따라 활성화 함수의 값이 일정하지 않게되고 따라서 층을 여러개 쌓을 수 없다고 한다.
GELU(Gaussian Error Linear Unit)
참고: https://89douner.tistory.com/22
http://cs231n.stanford.edu/2017/syllabus.html
'AI Tech' 카테고리의 다른 글
| [논문 리뷰] VGGNet (Very Deep Convolutional Networks for Large-Scale Image Recognition) 논문 리뷰 (2) | 2022.10.04 |
|---|---|
| Transfer Learning(전이 학습) (0) | 2022.09.02 |



